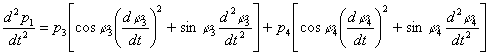Приложение III
Аналитическое  решение  для модуля Пл2

При исследовании кинематики механизмов векторные модели часто содержат контуры с двумя неизвестными по величине векторами, направленными параллельно координатным осям. На рис III.1 в качестве примера приведена кинематическая схема кривошипно-коромыслового механизма и три векторных контура, составляющих его векторную модель при решении задачи о движении центров масс s₁ и s₂ звеньев 1 и 2.

Рис.  III.1

Параметрическая формула рассматриваемой модели (рис. III.2) содержит два частных варианта модуля Пл2 - контуры II и  III, у которых  и  и  .  .

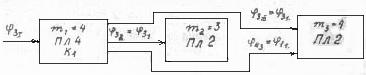
Рис.  III.2

Рассмотрим основные одноаргументные модули Пл2 с функциями p₁ и p₂ и постоянными параметрами  и . .

   Уравнения (6.4)-(6.5)  представим в виде

                                                                                                  (1)

                                                                                                   (2)

Тогда

и

(см. Рис III.1, в)  Из уравнений (1)-(2)

и

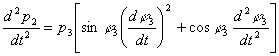
Рассмотрим основные двухаргументные модули Пл2 с функциями p₁ и p₂ и постоянными параметрами  и . .

. Из уравнений (1)-(2)

Тогда

и

. Из уравнений (6.4)-(6.5) представим в виде

                                                                                 (3)

                                                                                   (4)

Тогда

и

  Из уравнений (3)-(4)

и

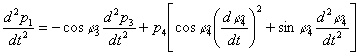
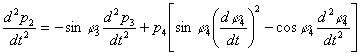
 (см. рис. III, г). Из уравнений (3)-(4)